바닥에 놓은 정팔면체를 위에서 보았을 때 어떤 모습으로 보일까요? 이 글에서는 정팔면체의 정사영에 대해 이야기하고, 이 것을 이용해 경우의 수와 공간도형 문제를 풀어봅니다.
바닥에 놓은 정팔면체는 위에서 보면 정육각형으로 보인다.
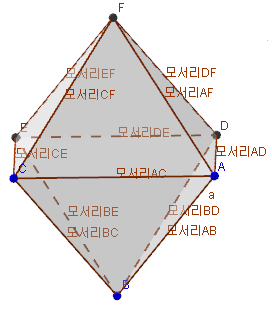
정팔면체의 한 면을 바닥에 놓고 위에서 보면 정육각형으로 보입니다. 즉 정팔면체를 정팔면체의 한 면과 평행한 면으로 정사영을 만들면 그 정사영은 정육각형이 됩니다. 다음 그림은 정팔면체의 한 면 FED를 바닥에 놓고 이 정팔면체를 위에서 본 모습을 그린 것입니다. (정팔면체의 모서리와 점의 위치를 정육각형에서 확인해보세요.)
[그림1]. 이 정팔면체를 바닥에 놓고 위에서 바라보면
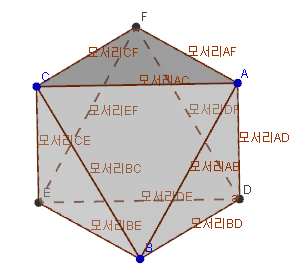
[그림2]. 이렇게 정육각형으로 보인다.
이때 정팔면체의 한 모서리의 길이를 \(a\)라고 하면 정6각형의 한 모서리의 길이는 \({\sqrt{3}\over 3}a\)가 됩니다. 이제 이 사실을 이용하여 다음 2문제를 풀어봅시다.
[문제1]
서로 다른 8개의 색을 모두 사용하여 정팔면체를 색칠하는 방법의 수는?해답
[그림2]를 참조하여 문제를 풀어봅시다. 먼저 8개의 색을 빨주노초파남보검이라고 해봅시다. 먼저 바닥에 있는 면FED를 특정한 색 (예를 들어 빨간색)으로 칠해 놓으면 나머지 면은 다음과 같은 순서로 정팔면체를 색칠할 수 있습니다.(1) 면FED 맞은 편에 있는 면 CBA는 남은 7가지 색 중 한 개의 색을 뽑아 칠할 수 있습니다.
(2) 그리고 남은 6개의 색 중 3개의 색을 뽑아 (\(_6C_3\)) FED에 인접한 3개의 면, 면CEF, 면EBD, 면AFD에 칠합니다.
(3) 이때 [그림3]과 같이 면FED의 중심으로 회전을 하게 되면 일치하는 경우가 생기게 됩니다. 즉 색칠을 하지 않은 상태에서 이 세 개의 면은 서로 구별이 되지 않습니다. 정육각형의 대칭성 때문입니다. 따라서 이 3개의 면을 색칠하는 방법의 수는 원순열의 수와 같습니다. 그러므로 이 3개의 면을 특정한 3개의 색으로 색칠하는 방법의 수는 \(2!\)입니다.
(4) 지금까지 5개의 면을 색칠했으므로 이제 3개의 면만 색칠하는 일만 남았습니다. 마지막으로 칠할 이 3개의 면은 (1)-(3)번까지의 과정에서 이미 색칠한 면에 의해 서로 구별이 되기 때문에 순열의 수와 같습니다. 따라서 이 3개의 면을 색칠하는 방법의 수는 \(3!\)입니다.
(1)~(4)의 과정을 종합하면 서로 다른 8개의 색으로 정팔면체를 색칠하면 모든 방법의 수는
$$7\times_6C_3\times2!\times3!=1680$$
가 됩니다.
[그림3]. 정육각형의 대칭성 : 왼쪽과 오른쪽의 색칠은 서로 같은 것입니다. 왼쪽 그림을 삼각형FED의 무게중심을 중심으로 시계방향으로 120\(^\circ\)회전하면 오른쪽 그림이 됩니다.
다음으로 공간도형의 문제를 풀어봅시다. 여기에서도 정팔면체를 위에서 보면 정육각형이 된다는 사실이 문제 해결의 중요한 원리가 됩니다.
[문제2]
[그림1]의 정8면체에서 면FED와 모서리FA, 면FED와 모서리 AB가 이루는 각 중 예각을 \(\theta_1\), \(\theta_2\)라 하자. \(\cos\theta_1\)과 \(\cos\theta_2\)의 값을 각각 구하시오.해답
이번에는 [그림1]과 [그림2] 모두 이용해 봅시다. [그림1]의 정팔면체의 한 모서리 길이를 \(a\)라고 정하면 모서리 FA와 모서리 AB의 길이는 모두 \(a\)가 됩니다. 하지만 [그림2]의 정육각형에서 선분 FA와 선분 AB의 길이는 각각 \({\sqrt{3}\over 3}a\)와 \(a\)가 됩니다. 그런데 이 정육각형은 정팔면체의 면FED위로의 정사영이므로 다음과 같은 식을 만들 수 있습니다.$$a\cos\theta_1={\sqrt{3}\over 3}a, \cos\theta_1={\sqrt{3}\over 3}$$
$$a\cos\theta_2=a, \cos\theta_2=1$$
이렇게 바닥에 놓인 정팔면체를 위에서 보면 정육각형이 된다는 것을 사용하여 여러 종류의 문제를 해결할 수 있었습니다. 이 사실을 이용한 다른 문제들도 있는데 다음 글에서 소개하겠습니다. 정팔면체를 직접 만들어서 확인해보세요!